(a)
Let:
w1 = Original width
l1 = Original length
w2 = New width
l2 = New length
A1 = Original area
A2 = New Area
so:
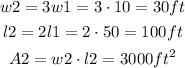
Answer:
New length: 100ft
New width: 30 ft
New Area: 3000ft²
-------------------------------------------
(b)
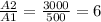
Answer:
The area of the new walkway will be 6 times the area of the current walkway
---------------------------------------
(c)
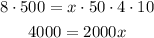
Solve for x:
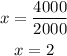
Answer:
Make the new length 2 times the current length.