To asnwer this questions we can use the binomial distribution. The probability of having a number k of successes in a binomial experiment is given by:
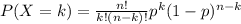
where n is the number of trials and p is the probability of succes.
a.
Since we like to have a one in each roll this means that in this case the probability of succes will be 1/6 (1 possibility out of 6). Also we have 8 rolls then n=8, and we like that the one is the result in each of them, then k=8. Plugging this values in the distribution we have:
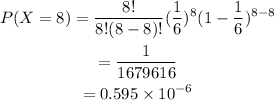
Therefore the probability of getting a one in each roll is 0.00000595.
b.
Since we like a 6 exactly twice this means that k=2. The probability of succes is 1/6. Plugging the values in the distribution we have:
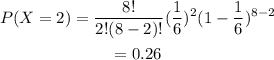
Therefore the probability of obtaining 6 exactly twice is 0.26.
c.
The probability of obtaining at least once a six is the sum of obtaining 1 and obtaining 2 and obtaining 3 and so on.
That means that the probability is:
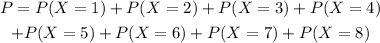
but this is more easily obtain if we notice that this is the same as:
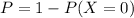
This comes from the fact that the sum of all the successes possibilities (in this case obtaining a 6) have to be 1.
Then the probability of obtaniing at least once a six is:
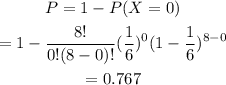
Therefore the probability of obtaining at least once a six is 0.767.