Question

11. A fair die is rolled 8 times. What is the probability of getting a. I on each of the 8 rolls? b. 6 exactly twice in the 8 rolls? c. 6 at least once in the 8 rolls?

Answer 1

To asnwer this questions we can use the binomial distribution. The probability of having a number k of successes in a binomial experiment is given by:

`P(X=k)=(n!)/(k!(n-k)!)p^k(1-p)^(n-k)`

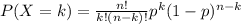
where n is the number of trials and p is the probability of succes.

a.

Since we like to have a one in each roll this means that in this case the probability of succes will be 1/6 (1 possibility out of 6). Also we have 8 rolls then n=8, and we like that the one is the result in each of them, then k=8. Plugging this values in the distribution we have:

`\begin{gathered} P(X=8)=(8!)/(8!(8-8)!)((1)/(6))^8(1-(1)/(6))^(8-8) \\ =(1)/(1679616) \\ =0.595*10^(-6) \end{gathered}`

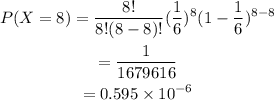
Therefore the probability of getting a one in each roll is 0.00000595.

b.

Since we like a 6 exactly twice this means that k=2. The probability of succes is 1/6. Plugging the values in the distribution we have:

`\begin{gathered} P(X=2)=(8!)/(2!(8-2)!)((1)/(6))^2(1-(1)/(6))^(8-2) \\ =0.26 \end{gathered}`

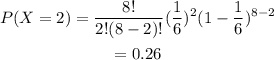
Therefore the probability of obtaining 6 exactly twice is 0.26.

c.

The probability of obtaining at least once a six is the sum of obtaining 1 and obtaining 2 and obtaining 3 and so on.

That means that the probability is:

`\begin{gathered} P=P(X=1)+P(X=2)+P(X=3)+P(X=4) \\ +P(X=5)+P(X=6)+P(X=7)+P(X=8) \end{gathered}`

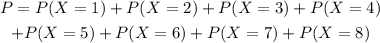
but this is more easily obtain if we notice that this is the same as:

`P=1-P(X=0)`

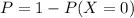
This comes from the fact that the sum of all the successes possibilities (in this case obtaining a 6) have to be 1.

Then the probability of obtaniing at least once a six is:

`\begin{gathered} P=1-P(X=0) \\ =1-(8!)/(0!(8-0)!)((1)/(6))^0(1-(1)/(6))^(8-0) \\ =0.767 \end{gathered}`

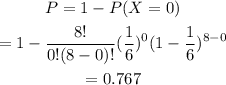
Therefore the probability of obtaining at least once a six is 0.767.