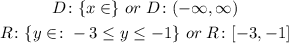Question

Using y= sin x OR y= cos x [Sinusoidal function] as the parent function, make your own transformations (5 units right, reflect on x axis, 2 units down, horizontal compression with factor 2). Then graph and state domain and range.

Answer 1

Using

`y=\sin (x)`

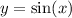
5 units right: Let's use the following rule:

`\begin{gathered} y=f(x-5) \\ so\colon \\ y=\sin (x-5) \end{gathered}`

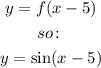
Reflect on x-axis: Let's use the following rule:

`\begin{gathered} y=-f(x) \\ so\colon \\ y=-\sin (x-5) \end{gathered}`

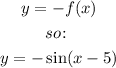
2 units down: Let's use the following rule:

`\begin{gathered} y=f(x)-2 \\ so\colon \\ y=-\sin (x-5)-2 \end{gathered}`

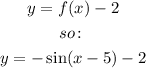
Horizontal compression with factor 2: Let's use the following rule:

`\begin{gathered} y=f(2x) \\ so\colon \\ y=-\sin (2x-5)-2 \end{gathered}`

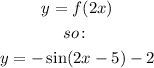
Let's graph the parent function, and the new function:

The blue graph is the parent function and the red graph is the new function after the transformations applied.

The domain and the range of the new function are:

`\begin{gathered} D\colon\mleft\lbrace x\in\R\mright\rbrace_{\text{ }}or_{\text{ }}D\colon(-\infty,\infty) \\ R\colon\mleft\lbrace y\in\R\colon-3\le y\le-1\mright\rbrace_{\text{ }}or_{\text{ }}R\colon\lbrack-3,-1\rbrack \end{gathered}`