Question

Find the mean, variance, and standard deviation for the data set. 19,11,21,9,15

Answer 1

Given:

The dataset : 19, 11, 21, 9, 15

Mean

The sum of the values divided by the number of values.

`\begin{gathered} mean\text{ = }(\sum_^x)/(n) \\ =\text{ }\frac{19\text{ + 11 + 21 +}9\text{ + 15}}{5} \\ =\text{ }(75)/(5) \\ =\text{ 15} \end{gathered}`

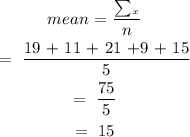
The mean is 15

Variance

Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value.

`\begin{gathered} variance\text{ = }(\sum^(x-x*)^2)/(n-1) \\ =\text{ }\frac{(19-15)^2\text{ + \lparen11-15\rparen}^2+(21-15)^2\text{ +}(9-15)^2\text{ + \lparen15-15\rparen}^2\text{ }}{5-1} \\ =\text{ 26} \end{gathered}`

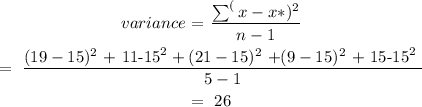
The variance is 26

Standard deviation

The standard deviation is square root of the variance

`\begin{gathered} \sigma\text{ = }√(26) \\ =\text{ 5.099} \\ \approx\text{ 5.10} \end{gathered}`

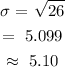
The standard deviation is 5.10