Question

Consider the following compound inequality. 2x+3_<5 or 4x+1>17A)Solve the inequality for x.B) Graph the compound inequality. C) Enter the solution in interval notation.

Answer 1

step 1

Solve the first inequality

`2x+3\leq5`
`\begin{gathered} 2x\leq5-3 \\ 2x\leq2 \\ x\leq1 \end{gathered}`

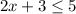
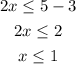
the solution for the first inequality is the interval (-infinite,1]

step 2

Solve the second inequality

4x+1>17

4x>16

x>4

the solution for the second inequality is the interval (4, infinite)

therefore

the solution of the compound inequality is

(-infinite,1] U (4, infinite)

In a number line, the solution is

At x=1 is a closed circle and at x=4 is an open circle