We can calculate the interest as the difference between the future and the present value of the investment:
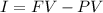
The present value is $4780.
The annual interest rate is r=1.25/100=0.0125.
The number of years is 8, so n=8.
We can calculate the future value as:
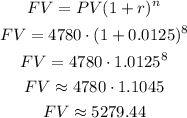
Then, we can calculate the interest as:
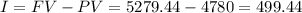
Answer: D. $499.44