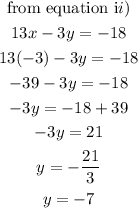Given the pair of simultaneous equation;
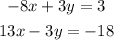
We are going to use the method of elimination to solve this.
We will be eliminating the variable y first, since it has the same co-efficient in the two(2) equations.
Thus, we have:
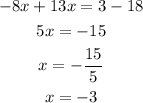
To solve for y, we are going to substitute for x = -3 into any of the two(2) equations.
Thus, we have: