The inequality is given as,
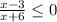
Note that the denominator can never be zero otherwise the rational function would become indeterminate. So we have to exclude the value at which the denominator,
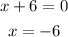
So the function is not defined at x = - 6.
Consider that the division of the numbers can be non-positive, only if exactly one of the numbers is non-positive.
So we have to obtain the interval in which one of the factors is positive and the other is negative.
CASE-1: When the numerator is positive and the denominator is negative,