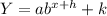
If b > 1 then it's an exponential growth
If b < 1 then it's an exponential decay
Y = 3(1/2)^(x+3) decay
Y = 4^(x-3) + 6 growth
Y = -2^x - 5 decay
Y = (2/3)^(x-2) +1 decay
The y-intercept is found replacing x = 0 into the equation.
Y = 3(1/2)^(0+3)
Y = 3(1/2)^3
Y = 3(1/8)
Y = 3/8
Y = 4^(0-3) + 6
Y = 4^(-3) + 6
Y = 1/64 + 6
Y = 385/64
Y = -2^0 - 5
Y = -1 - 5
Y = -6
Y = (2/3)^(0-2) +1
Y = (2/3)^(-2) +1
Y = (3/2)^(2) +1
Y = 9/4 +1
Y = 13/4
The vertical movement is found identifying k in the equations.
Y = 3(1/2)^(x+3) k = 0 no vertical move
Y = 4^(x-3) + 6 k = 6 vertical move 6 units up
Y = -2^x - 5 k = -5 vertical move 5 units down
Y = (2/3)^(x-2) +1 k = 1 vertical move 1 unit up
If the equation is flipped or not is seen in the a parameter. If a < 0, it's flipped, if a > 0, it isn't flipped
Y = 3(1/2)^(x+3) a > 0 not flipped
Y = 4^(x-3) + 6 a > 0 not flipped
Y = -2^x - 5 a < 0 flipped
Y = (2/3)^(x-2) +1 a > 0 not flipped
The range is found with help of the vertical move and the flip
Y = 3(1/2)^(x+3) no vertical move, not flipped range: [0, ∞]
Y = 4^(x-3) + 6 vertical move 6 units up, not flipped range: [6, ∞]
Y = -2^x - 5 vertical move 5 units down range: [-5, -∞]
Y = (2/3)^(x-2) +1 vertical move 1 unit up, not flipped range: [1, ∞]
The horizontal movement is found identifying h in the equations.
Y = 3(1/2)^(x+3) h = 3 horizontal move 3 units left
Y = 4^(x-3) + 6 h = -3 horizontal move 3 units right
Y = -2^x - 5 h = 0 no vertical move
Y = (2/3)^(x-2) +1 h = -2 horizontal move 2 units right
If the equation is stretched or shrunk is seen in the a parameter. If a > 1, the function stretches, if 0 < a < 1, 1, the function shrinks
Y = 3(1/2)^(x+3) a = 3 stretches
Y = 4^(x-3) + 6 a = 1 doesn't stretch nor shrink
Y = -2^x - 5 a = -1 doesn't stretch nor shrink
Y = (2/3)^(x-2) +1 a = 2/3 shrinks