The definition of the cosecant function is

Therefore,
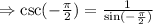
To find sin(-pi/2), use the diagram below.
Consider that the circumference has a radius equal to 1. Then, the coordinates of the orange point are (0,-1). Furthermore, the points on the circumference are given as (cos(theta), sin(theta)); therefore,
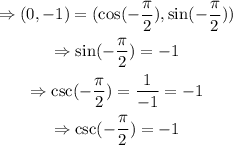
Thus, the answer is csc(-pi/2)=-1