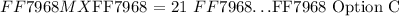Question

I need help solving this I thought it was 7 but I’m not too sure now

Answer 1

We are given a triangle such that two line segments are drawn as medians:

`MX\text{ and YL are median lines}`

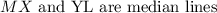
A meadian line has three points that are off importance as follows:

`\begin{gathered} \text{Strats from one of the vertex of a triangle} \\ \text{Passes through the centroid of the triangle} \\ Bi\sec ts\text{ the opposite side of the triangle} \end{gathered}`

Hence, using the above information we can extract that:

`\begin{gathered} Y\text{ is the mid-point of MK} \\ X\text{ is the mid-point of KL} \\ \text{\textcolor{#FF7968}{AND}} \\ A\text{ is the centroid of the entire triangle} \end{gathered}`

We can also use the properties of median length that states:

`\begin{gathered} \text{Length from vertex to centroid : Centroid to bisection point of opposite side} \\ \end{gathered}`

The ratio of the above two lengths for any median line of a triangle remains true for:

`2\text{ : 1}`

This means that the line segment from centroid to bisection ( mid ) point of the opposite side is shorter than the preceeding length; hence, the ratio is ( 2 : 1 ).

We are given the length of the line segment MA the larger part of the median line:

`MA\text{ = 14 units}`

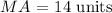
We can use the property of ratio of lengths for the median lines and determine the length of the smaller part of the median line as follows:

`\begin{gathered} \text{ 2 : 1} \\ MA\text{ : AX} \\ ======== \\ AX\text{ = }(MA)/(2) \\ \\ AX\text{ = }(14)/(2)\text{ = 7 units} \end{gathered}`

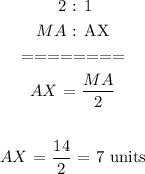
From the above property we determined the length of the shorter line segment. Now we have lengths for the both constituent line segments of median line ( MX ). We can simply sum the individual lengths as follows:

`\begin{gathered} MX\text{ = AX + MA} \\ MX\text{ = 7 + 14} \\ \textcolor{#FF7968}{MX}\text{\textcolor{#FF7968}{ = 21 units}} \end{gathered}`

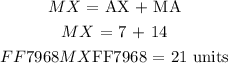
Hence, the answer is:

`\textcolor{#FF7968}{MX}\text{\textcolor{#FF7968}{ = 21 }}\textcolor{#FF7968}{\ldots}\text{\textcolor{#FF7968}{ Option C}}`