Step 1
Given;

Step 2
Draw the diagram
Step 2
Calculate the measure of angle PQR
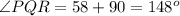
This is because using alternate exterior angles are equal theorem, the first part of angle Q 58 degrees. Since R is due east of Q, then the other part must be 90 degrees, when summed we get 148 degrees
Step 3
Calculate the distance PR. To do this we will use the cosine rule
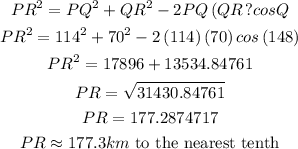
Step 4
Calculate the bearing of P from R.
Use sine rule and find angle R
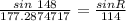
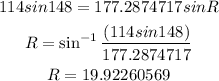
The bearing of P from R = (90-angle R)+90+90=250 degrees approximately to the nearest whole number
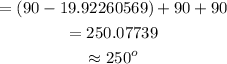
The bearing of P from R =250 degrees approximately to the nearest whole number