Question

1. P, Q and R are three buildings. A car began its journey at P, drove to Q, then to R and returned to P. The bearing of Q from P is 058º and R is due east of Q. PQ = 114 km and QR = 70 km. © Draw a clearly labelled diagram to represent the above informationen on the diagram TƏRund (a) the north/south direction (b) the bearing 058° (c) the distances 114 km and 70 km. (ii) Calculate (a) the measure of angle POR (b) the distance PR [3] (c) the bearing of P from R [3]

Answer 1

Step 1

Given;

`\begin{gathered} The\text{ bearing of Q from P is 058}^o\text{ } \\ R\text{ is due east of Q} \\ PQ=114km \\ QR=70km \end{gathered}`

Step 2

Draw the diagram

Step 2

Calculate the measure of angle PQR

`\angle PQR=58+90=148^o`

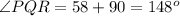
This is because using alternate exterior angles are equal theorem, the first part of angle Q 58 degrees. Since R is due east of Q, then the other part must be 90 degrees, when summed we get 148 degrees

Step 3

Calculate the distance PR. To do this we will use the cosine rule

`\begin{gathered} PR^2=PQ^2+QR^2-2PQ\left(QR\right?cosQ \\ PR^2=114^2+70^2-2\left(114\right)\left(70\right)cos\left(148\right) \\ PR^2=17896+13534.84761 \\ PR=√(31430.84761) \\ PR=177.2874717 \\ PR\approx177.3km\text{ to the nearest tenth} \end{gathered}`

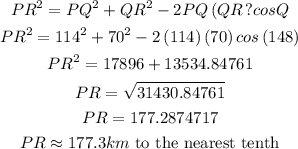
Step 4

Calculate the bearing of P from R.

Use sine rule and find angle R

`\frac{sin\text{ 148}}{177.2874717}=(sinR)/(114)`
`\begin{gathered} 114sin148=177.2874717sinR \\ R=\sin^(-1)(\mleft(114sin148\mright))/(177.2874717) \\ R=19.92260569 \end{gathered}`

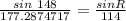
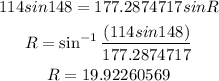
The bearing of P from R = (90-angle R)+90+90=250 degrees approximately to the nearest whole number

`\begin{gathered} =\left(90-19.92260569\right)+90+90 \\ =250.07739 \\ \approx250^o \end{gathered}`

The bearing of P from R =250 degrees approximately to the nearest whole number