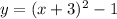From the image.
we have
1 y
1 x^2
6 x
8 (1squares)
We can write the standard equation as

But we need to express it in vertex form y = a(x-h)^2 + k where (h,k) is the vertex
to complete the squares we need to express the equation as
y = (x^2+6x+8+__)-___
to complete the square we need to add +1 inside the parenthesis and -1 outside
y = (x^2+6x+8+1)-1
We can express the equation
y = (x+3)^2 -1