SOLUTION
We want to solve the question with elimination method
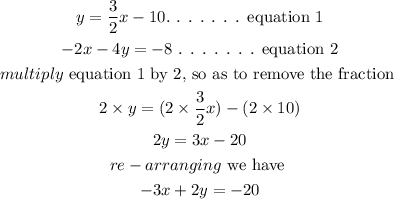
So our paired equation becomes

To eliminate y, multiply the upper equation by 4 and the lower by 2, we have
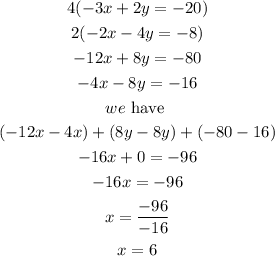
So put x for 6 into the second equation, we have
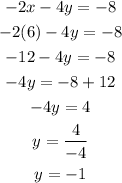
Hence x = 6 and y = -1
The graph is shown below
Hence the point of intersection is (6, -1)