Question

Are [3/6 -4/5] and [5/-6 4/3] inverses? Why or why not?

Answer 1

A.

Step-by-step explanation:

Two matrices are inverses if when we multiply them, we get the identity matrix with 1 in the diagonal and 0 on the other entries.

In this case, we get that the multiplication of the matrices is equal to

`\begin{bmatrix}{3} & {-4} \\ {6} & {5}\end{bmatrix}\begin{bmatrix}{5} & {4} \\ {-6} & {3}\end{bmatrix}=\begin{bmatrix}{3(5)-4(-6)} & {3(4)-4(3)} \\ {6(5)+5(-6)} & {6(4)+5(3)}\end{bmatrix}=\begin{bmatrix}{15+24} & {12-12} \\ {30-30} & {24+15}\end{bmatrix}=\begin{bmatrix}{39} & {0} \\ {0} & {39}\end{bmatrix}`

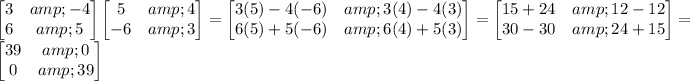
Since

`\begin{bmatrix}{39} & {0} \\ {0} & {39}\end{bmatrix}\\e\begin{bmatrix}{1} & {0} \\ {0} & {1}\end{bmatrix}`

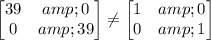
We get that the matrices are not inverses.

So, the answer is A.