Question

Hi I need help with these problems only 1 and 3 since my teacher told us to do even number and if I don't know what to do at all

Answer 1

Since we are dealing with a right triangle, we can use the following trigonometric identities

`\sin \theta=(O)/(H),\cos \theta=(A)/(H)`

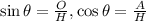
Where θ is an inner angle (different than 90°) of the triangle, O is the opposite side to θ, A is the adjacent side to θ, and H is the hypotenuse.

a) In our case,

`\begin{gathered} \theta=30\text{degre}e \\ H=14,A=m,O=n \\ \Rightarrow\sin (30degree)=(n)/(14) \\ \Rightarrow n=14\cdot\sin (30degree)=14\cdot0.5=7 \\ \Rightarrow n=7 \end{gathered}`

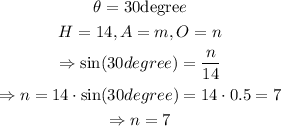
and

`\begin{gathered} \Rightarrow\cos (30degree)=(m)/(14) \\ \Rightarrow m=14(\cos (30degree))=14\cdot\frac{\sqrt[]{3}}{2}=7\sqrt[]{3} \\ \Rightarrow m=7\sqrt[]{3} \end{gathered}`

The answers are n=7 and m=7sqrt(3).

3) In a diagram, the problem states

Using the same trigonometric identities mentioned in part 1) (plus the tangent function), we get

`\begin{gathered} \sin (30degree)=(18)/(H),\tan (30degree)=(18)/(A) \\ \Rightarrow H=(18)/(\sin(30degree)),A=(18)/(\tan(30degree))=\frac{18}{\frac{1}{\sqrt[]{3}}}=18\sqrt[]{3} \\ \Rightarrow H=(18)/(0.5)=36,A=18\sqrt[]{3} \\ \Rightarrow H=36,A=18\sqrt[]{3} \end{gathered}`

The hypotenuse is equal to 36 ft, and the other leg is equal to 18sqrt(3) ft