Question

A teenager in a highrise building looks out his window at another building across the street and realizes a crime is being committed. If the buildings are 60 feet apart, and the teenager is looking down into the other building with an angle of depression of 20°, how many feet lower is the floor where the crime is being committed? If each floor is 10 feet, about how many floors down is it?

Answer 1

Hello!

The first step to solving this exercise is to draw the situation, look:

Now we can solve this exercise. Notice that we want to know the height that I called "X".

To find it, we must use the tangent of 20º, look:

`\tan (20\degree)=(opposite)/(adjacent)`
`\begin{gathered} (0.364)/(1)=(60)/(x) \\ \\ 0.364x=60 \\ x=(60)/(0.364) \\ \\ x\cong164.83 \end{gathered}`

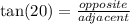
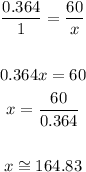
If each floor is 10 feet:

`(164.83)/(10)=16.483\text{ floors}`

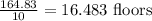
If you have to approximate, you can say that it is 16.5 floors down.