Question

You have $500,000 saved for retirement. Your account earns 8% interest. How much will you be able to pullout each month, if you want to be able to take withdrawals for 15 years?$

Answer 1

The rule of the payout annuity is

`P=(d(1-(1+(r)/(n))^(-nt)))/((r)/(n))`

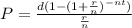
P is the initial amount

d is regular withdrawals

r is the annual rate in decimal

n is the number of periods in a year

t is the time

Since you have $500 000 saved, then

P = 500000

Since the interest is 8%, then

r = 8/100 = 0.08

Since the time is 15 years, then

t = 15

Since you want the monthly amount, then

n = 12

Substitute them in the rule to find d

`\begin{gathered} 500000=(d(1-(1+(0.08)/(12))^(-12(15))))/((0.08)/(12)) \\ 500000((0.08)/(12))=d(1-((151)/(150))^(-180)) \\ (10000)/(3)=d(1-((151)/(150))^(-180)) \\ ((10000)/(3))/((1-((151)/(150))^(-180)))=d \\ 4778.260422=d \end{gathered}`

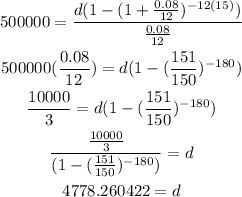
Then you will be able to pull $4778.260422 each month