The rule of the payout annuity is
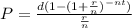
P is the initial amount
d is regular withdrawals
r is the annual rate in decimal
n is the number of periods in a year
t is the time
Since you have $500 000 saved, then
P = 500000
Since the interest is 8%, then
r = 8/100 = 0.08
Since the time is 15 years, then
t = 15
Since you want the monthly amount, then
n = 12
Substitute them in the rule to find d
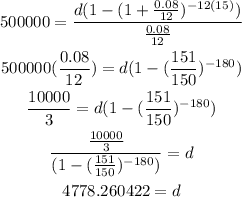
Then you will be able to pull $4778.260422 each month