If we graph the given points, we have:
One property of the parallelograms is that their opposite sides are equal.
Then, we have to verify if the segments QT and RS are equal.
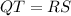
To find the measure of segments QT and RS, we can use the distance formula.
![\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}\Rightarrow\text{ Distance formula} \\ \text{ Where} \\ (x_1,y_1)\text{ and }(x_2,y_2)\text{ are the coordinates of the points} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/l7vlyt222jz7cdek5q8j69andiuid27jin.png)
• Measure of segment QT
![\begin{gathered} (x_1,y_1)=Q(-10,-2) \\ (x_2,y_2)=T(-11,-8) \\ d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ d=\sqrt[]{(-11-(-10))^2+(-8-(-2))^2} \\ d=\sqrt[]{(-11+10)^2+(-8+2)^2} \\ d=\sqrt[]{(-1)^2+(-6)^2}\rbrack \\ d=\sqrt[]{1+36} \\ d=\sqrt[]{37} \\ d\approx6.08\Rightarrow\text{ The symbol }\approx\text{ is read 'approximately'} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/a1nacfm2fags2skxxbgla1u19v7im4q3k0.png)
• Measure of segment RS
![\begin{gathered} (x_1,y_1)=R(1,-1) \\ (x_2,y_2)=S(1,-7) \\ d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ d=\sqrt[]{(1-1)^2+(-7-(-1))^2} \\ d=\sqrt[]{(0)^2+(-7+1)^2} \\ d=\sqrt[]{0+(-6)^2} \\ d=\sqrt[]{(-6)^2} \\ d=\sqrt[]{36} \\ d=6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/49p8n1jjy6ngwmn6cb4stsngqgbszgnjr0.png)
As we can see, the segments QT and RS are different.
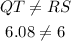
Then, the figure does not satisfy the mentioned property of parallelograms.
Therefore, the figure is not a parallelogram.