Question

can you help me on this one?I need to determine whether the figure is a parallelogram using the distance formula.

Answer 1

If we graph the given points, we have:

One property of the parallelograms is that their opposite sides are equal.

Then, we have to verify if the segments QT and RS are equal.

`QT=RS`

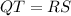
To find the measure of segments QT and RS, we can use the distance formula.

`\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}\Rightarrow\text{ Distance formula} \\ \text{ Where} \\ (x_1,y_1)\text{ and }(x_2,y_2)\text{ are the coordinates of the points} \end{gathered}`

• Measure of segment QT

`\begin{gathered} (x_1,y_1)=Q(-10,-2) \\ (x_2,y_2)=T(-11,-8) \\ d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ d=\sqrt[]{(-11-(-10))^2+(-8-(-2))^2} \\ d=\sqrt[]{(-11+10)^2+(-8+2)^2} \\ d=\sqrt[]{(-1)^2+(-6)^2}\rbrack \\ d=\sqrt[]{1+36} \\ d=\sqrt[]{37} \\ d\approx6.08\Rightarrow\text{ The symbol }\approx\text{ is read 'approximately'} \end{gathered}`

• Measure of segment RS

`\begin{gathered} (x_1,y_1)=R(1,-1) \\ (x_2,y_2)=S(1,-7) \\ d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ d=\sqrt[]{(1-1)^2+(-7-(-1))^2} \\ d=\sqrt[]{(0)^2+(-7+1)^2} \\ d=\sqrt[]{0+(-6)^2} \\ d=\sqrt[]{(-6)^2} \\ d=\sqrt[]{36} \\ d=6 \end{gathered}`

As we can see, the segments QT and RS are different.

`\begin{gathered} QT\\e RS \\ 6.08\\e6 \end{gathered}`

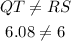
Then, the figure does not satisfy the mentioned property of parallelograms.

Therefore, the figure is not a parallelogram.