Question

In the diagram of △△ADC below, EB∥∥DC, AE=2, AB=10, and BC=45. What is the length of AD?

Answer 1

11 units

Step-by-step explanation:

Given that lines EB and DC are parallel, we use the proportional division theorem:

`(AE)/(ED)=(AB)/(BC)`

Substitute the given values:

`\begin{gathered} (2)/(ED)=(10)/(45) \\ \text{Cross multiply} \\ ED*10=2*45 \\ \text{Divide both sides by 10} \\ (ED*10)/(10)=(2*45)/(10) \\ ED=9 \end{gathered}`

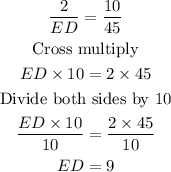
Next, find the length of AD:

`\begin{gathered} AD=AE+ED \\ =2+9 \\ =11\text{ units} \end{gathered}`

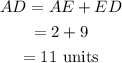
The length of AD is 11 units.

Alternate Method

`ED=AD-2`

So, we have that:

`(AE)/(ED)=(AB)/(BC)\implies(AE)/(AD-2)=(AB)/(BC)`

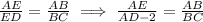
Substitute the given values:

`(2)/(AD-2)=(10)/(45)`

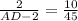
Cross multiply: