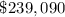Question

The weekly revenue for a product is given by R(x)=307.8x−0.045x2, and the weekly cost is C(x)=10,000+153.9x−0.09x2+0.00003x3, where x is the number of units produced and sold.(a) How many units will give the maximum profit?(b) What is the maximum possible profit?

Answer 1

The number of units that will give the maximum profit is;

`1900\text{ units}`

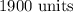
The maximum possible profit is;

`\text{ \$}239,090`

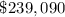
Step-by-step explanation:

Given that the weekly revenue for a product is given by ;

`R(x)=307.8x-0.045x^2`

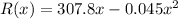
and the weekly cost is ;

`C(x)=10,000+153.9x-0.09x^2+0.00003x^3`

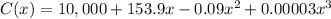
Recall that

Profit = Revenue - Cost

`P(x)=R(x)-C(x)`
`\begin{gathered} P(x)=307.8x-0.045x^2-(10,000+153.9x-0.09x^2+0.00003x^3) \\ P(x)=307.8x-0.045x^2-10,000-153.9x+0.09x^2-0.00003x^3 \\ P(x)=153.9x+0.045x^2-0.00003x^3-10,000 \end{gathered}`

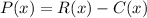
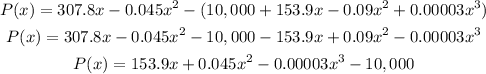
Using graph to derive the maximum point on the function;

Therefore, the maximum point is at the point;

`(1900,239090)`

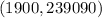
So;

The number of units that will give the maximum profit is;

`1900\text{ units}`

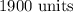
The maximum possible profit is;

`\text{ \$}239,090`