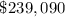Answer:
The number of units that will give the maximum profit is;
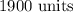
The maximum possible profit is;
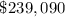
Step-by-step explanation:
Given that the weekly revenue for a product is given by ;

and the weekly cost is ;
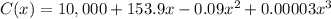
Recall that
Profit = Revenue - Cost

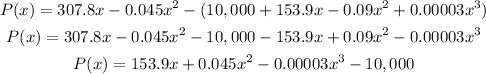
Using graph to derive the maximum point on the function;
Therefore, the maximum point is at the point;
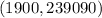
So;
The number of units that will give the maximum profit is;
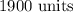
The maximum possible profit is;