Given two parallel lines and a transversal
The given angles: (2x-8) and (9x-10) are supplementary angles
So, the sum of the angles = 180
So,
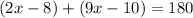
Solve the equation to find x :
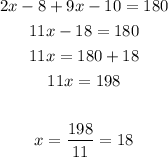
So, the answer will be x = 18
The converse of the solution:
when x = 18
So, the measure of the angles will be:
2x - 8 = 2 * 18 - 8 = 36 - 8 = 28
9x - 10 = 9 * 18 - 10 = 162 - 10 = 152
The sum of the angles are = 28 + 152 = 180
So, the sum of the angles = 180
So, the angles are supplementary angles
So, the lines J and K are parallel lines
so, J || K