Usa la ley de seno para hallar la medida del angulo B:
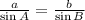
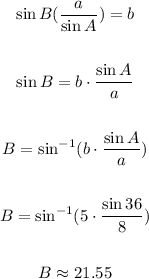
Como la suma de los angulos interiores de un triangulo siempre es 180°, usa la medida del angulo A y angulo B para hallar la medida del angulo C:
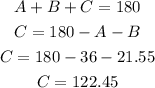
Usa la ley de seno para hallar la medida del lado c:
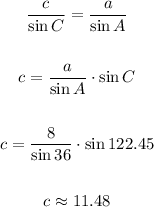
Entonces, las medidas que tenias que hallar so;
B=21.55°
C=122.45°
c=11.48