Okay, here we have this:
Considering the provided points, we are going to write a cubic function with these points as roots, so we have this:
The factored function will be equal to the multiplication of three binomials, where the first term will be x and the second will be each root with an inverse sign. Then we have:
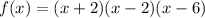
Now we are going to operate each term to obtain the expanded function:
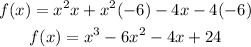
The last one we write is the function we are looking for and satisfies the requested roots.