Question

A 5000. kg elevator accelerates at 3.0m/s? as it begins to move upward. Calculate the tension in the cable

Answer 1

Given data;

* The mass of the elevator is 5000 kg.

* The acceleration of the elevator is,

`a=3ms^(-2)`

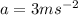
Solution:

The free body diagram of the elevator is,

The weight of the elevator is,

`W=mg`

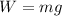
where m is the mass of the elevator and g is the acceleration due to gravity,

Substituting the known values,

`\begin{gathered} W=5000*9.8 \\ W=49000\text{ N} \end{gathered}`

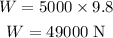
The net force acting on the elevator is,

`F_{\text{net}}=ma`

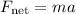
where a is the acceleration of the elevator moving upwards,

Substituting the known values,

`\begin{gathered} F_{\text{net}}=5000*3 \\ F_{\text{net}}=15000\text{ N} \end{gathered}`

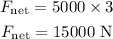
From the free body diagram, the tension acting on the cable is,

`\begin{gathered} T-W=F_{\text{net}} \\ T=F_{\text{net}}+W \end{gathered}`

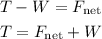
Substituting the known values,

`\begin{gathered} T=15000+49000 \\ T=64000\text{ N} \\ T=64\text{ kN} \end{gathered}`

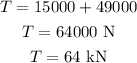
Thus, the tension acting in the cable is 64 kN.