Question

The siren of a burglar alarm system has a frequency of 960Hz . During a patrol a security officer, traveling in his car , hears the siren of the alarm of a house and approaches the house at a constant velocity. A detector in his car registers the frequency of the sound as 1000 Hz . Calculate the speed at which the patrol car approaches the house . Use the speed of sound in air as 340m.s

Answer 1

14.2 m/s

Step-by-step explanation:

When the source and receiver are getting closer, we can use the following equation:

`f_o=((v+v_o)/(v-v_s))f_s`

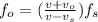
Where fo is the observed frequency, fs is the emitted frequency, vo is the speed of the observed, vs is the speed of the source, and v is the speed of the sound. Solving for vo, we get:

`\begin{gathered} (f_o)/(f_s)=(v+v_o)/(v-v_s) \\ \\ (f_o)/(f_s)(v-v_s)=v+v_o \\ \\ (f_o)/(f_s)(v-v_s)-v=v_o \\ \\ v_o=(f_o)/(f_s)(v-v_s)-v \end{gathered}`

Then, replacing v = 340 m/s, vs = 0 m/s, fs = 960 Hz, and fo = 1000 Hz, we get:

`\begin{gathered} v_r=(1000)/(960)(340-0)-340 \\ \\ v_r=14.2\text{ m/s} \end{gathered}`

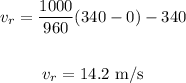
Therefore, the speed of the patrol car is 14.2 m/s