Answer:
14.2 m/s
Step-by-step explanation:
When the source and receiver are getting closer, we can use the following equation:
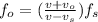
Where fo is the observed frequency, fs is the emitted frequency, vo is the speed of the observed, vs is the speed of the source, and v is the speed of the sound. Solving for vo, we get:
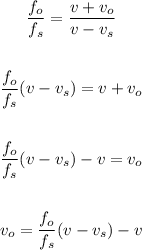
Then, replacing v = 340 m/s, vs = 0 m/s, fs = 960 Hz, and fo = 1000 Hz, we get:
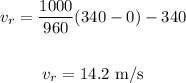
Therefore, the speed of the patrol car is 14.2 m/s