We are given the initial function to be
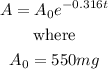
Page 5
Question 4
We are told to use the function above to estimate how long it will take for the amount in the body to be 175mg.
This simply translates to making A= 175 in the equation so that we will obtain
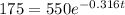
So we will make t the subject of the formula
To do so, we can follow the steps below
Step 1: Divide both sides by 550
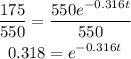
Next, we will take the natural logarithm to both sides
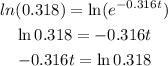
Next, we will divide both sides by -0.316
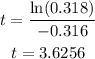
Thus, the value of t = 3.6256 hours.