Question

I am attaching pages 3-5 for context. I just need help with Question 4 on page 5. I have also attached my answers to page 3 (spreadsheet) and page 4 (screenshot).

Answer 1

We are given the initial function to be

`\begin{gathered} A=A_0e^(-0.316t) \\ \text{where} \\ A_0=550mg \end{gathered}`

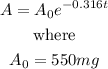
Page 5

Question 4

We are told to use the function above to estimate how long it will take for the amount in the body to be 175mg.

This simply translates to making A= 175 in the equation so that we will obtain

`175=550e^(-0.316t)`

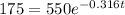
So we will make t the subject of the formula

To do so, we can follow the steps below

Step 1: Divide both sides by 550

`\begin{gathered} (175)/(550)=(550e^(-0.316t))/(550) \\ 0.318=e^(-0.316t) \end{gathered}`

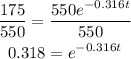
Next, we will take the natural logarithm to both sides

`\begin{gathered} ln(0.318)=\ln (e^(-0.316t)) \\ \ln 0.318=-0.316t \\ -0.316t=\ln 0.318 \end{gathered}`

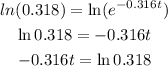
Next, we will divide both sides by -0.316

`\begin{gathered} t=(\ln (0.318))/(-0.316) \\ t=3.6256 \end{gathered}`

Thus, the value of t = 3.6256 hours.