Question

CourcesKhan AcademyEmpirical ruleYou might need: CalculatorThe lifespans of seals in a particular zoo are normally distributed. The average seal lives 13.8 years, the standarddeviation is 3.2 years,ALCROLUse the empirical rule (68 - 95 - 99.7%) to estimate the probability of a seal living less than 7.4 years.Asi%Show CalculatorTATUSCoReport a problemStuck? Watch a video or use a hint.SAPro

Answer 1

Answer:

Probability of a seal living less than 7.4 years, P(X < 7.4) = 0.023

Explanations:

The distribution is said to be a normal distributuion.

For a normal distribution, you first calculate the z value.

`\begin{gathered} \text{Average life, }\mu\text{ = 13.8} \\ \text{Standard Deviation, }\sigma\text{ = 3.2} \\ \text{The observed value, x = 7.4} \end{gathered}`

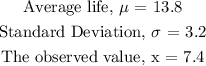
The z value is calculated as:

`\begin{gathered} \text{z = }\frac{\text{x -}\mu}{\sigma} \\ z\text{ = }(7.4-13.8)/(3.2) \\ z\text{ = }(-6.4)/(3.2) \\ z\text{ = -2} \end{gathered}`

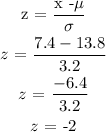
The probability of a seal living less than 7.4 years can be represented mathematically as:

P ( X < 7.4) Which can be interpreted as P(z < -2)

Checking this is in standard normal table:

P( z < -2) = 0.02275

Approximating to 3 decimal places, P(z < -2) = 0.023

Therefore, P ( X < 7.4) = 0.023