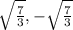Solution
The given function is
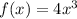
With given interval
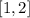
The function is differentiable on the open interval (1,2) and it is continuous on the closed interval [1,2]
Therefore mean value theorem can be used
Calculating the c value iit follows:
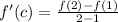
This gives
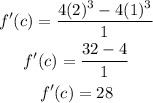
Differentiating the given function gives:
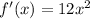
Equate f'(c) and f'(x)
This gives
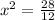
Solve the equation for x
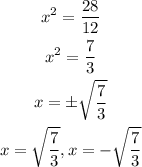
Therefore the values of c are