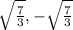Question

Determine whether the Mean Value theorem can be applied to f on the closed interval [a, b]. (Select all that apply.)

Answer 1

The given function is

`f(x)=4x^3`

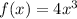
With given interval

`\lbrack1,2\rbrack`

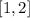
The function is differentiable on the open interval (1,2) and it is continuous on the closed interval [1,2]

Therefore mean value theorem can be used

Calculating the c value iit follows:

`f^(\prime)(c)=(f(2)-f(1))/(2-1)`

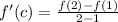
This gives

`\begin{gathered} f^(\prime)(c)=(4(2)^3-4(1)^3)/(1) \\ f^(\prime)(c)=(32-4)/(1) \\ f^(\prime)(c)=28 \end{gathered}`

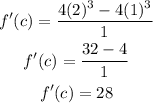
Differentiating the given function gives:

`f^(\prime)(x)=12x^2`

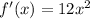
Equate f'(c) and f'(x)

This gives

`x^2=(28)/(12)`

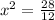
Solve the equation for x

`\begin{gathered} x^2=(28)/(12) \\ x^2=(7)/(3) \\ x=\pm\sqrt{(7)/(3)} \\ x=\sqrt{(7)/(3)},x=-\sqrt{(7)/(3)} \end{gathered}`

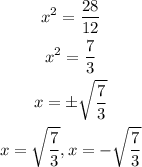
Therefore the values of c are

`\sqrt{(7)/(3)},-\sqrt{(7)/(3)}`