Question

The n = 3 row of Pascal's Triangle has the following entries: 1, 3, 3, and 1TrueFalse

Answer 1

Ok, in the Pascal Triangle, the element in the row number n and column number p is given by:

So let's take n=3 and find all the entries of that row. We are going to use 0, 1, 2 and 3 as possible values for p.

For p=0:

`(3!)/(0!(3-0)!)=(6)/(1\cdot3!)=(6)/(6)=1`

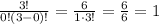
For p=1:

`(3!)/(1!\cdot(3-1)!)=(6)/(2!)=(6)/(2)=3`

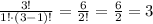
For p=2:

`(3!)/(2!\cdot(3-2)!)=(6)/(2\cdot1!)=(6)/(2)=3`

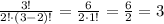
And for p=3:

`(3!)/(3!\cdot(3-3)!)=(3!)/(3!\cdot0!)=(3!)/(3!)=1`

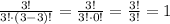
So the four entries in the third row of Pascal's Triangle are 1, 3, 3 and 1 so the statement is true.