Here we have the following parabola:
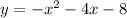
To find the vertex, we could use the following formula:
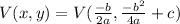
Where a, b and c are the coefficients of the quadratic function:

As you can see, in this problem a = -1 , b = -4 and c = -8. Thus,
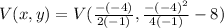
This is:
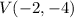
Then, the vertex of the parabola is (-2,-4)
The axis of symmetry of the parabola is the line x=-2. Since the vertex is situated at the coordinates (-2,-4), that means that the parabola is symmetrical around this line.
The vertex is maximum point of the parabola.
The range, is defined as all the values that the y-axis could take. If we notice, that is:
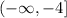
I'm going to upload a picture of the parabola: