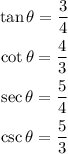Question

Please explain cos-cot equations. Then I would like to figure out the rest.If sin θ=3/5 and θ is in quadrant II, thencos(θ)=________ ;tan(θ)=________ ;cot(θ)=_________;sec(θ)=_________;csc(θ)=_________;Give exact values.

Answer 1

Remember that the sine of an angle in a right triangle is equal to the quotient between the side opposite to the angle and the hypotenuse of the triangle.

Since the sine of the given angle θ is equal to 3/5, we can represent θ as part of a right triangle whose hypotenuse has a measure of 5 and the side opposite to θ has a measure of 3:

The length of the side adjacent to θ must be equal to 4 in order to satisfy the Pythagorean Theorem:

`3^2+4^2=5^2`

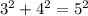
On the other hand, the cosine of an angle is defined as the quotient between the side adjacent to the angle and the hypotenuse of the triangle. Then, the cosine of θ must be equal to 4/5:

`\cos \theta=(4)/(5)`

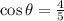
The rest of the trigonometric relations are defined in terms of the sine and the cosine as follows:

`\begin{gathered} \tan \theta=(\sin \theta)/(\cos \theta) \\ \cot \theta=(\cos \theta)/(\sin \theta) \\ \sec \theta=(1)/(\cos \theta) \\ \csc \theta=(1)/(\sin \theta) \end{gathered}`

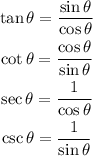
Since sinθ=3/5 and cosθ=4/5, then:

`\begin{gathered} \tan \theta=(3)/(4) \\ \cot \theta=(4)/(3) \\ \sec \theta=(5)/(4) \\ \csc \theta=(5)/(3) \end{gathered}`