Sides:
5n
12n
13n
If n is 1 the triangle have sides: 5, 12, 13
The converse of the pythagorean theorem is: If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle:

Then, a triangle with sides 5, 12, 13 is a right triangle.
If n is 2 the triangle have sides: 10,24, 26
converse of the pythagorean theorem:
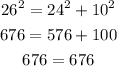
Triangle with n=1 and n=2 are similars as the ratio between corresponding side is equal:
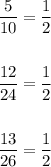
Then, with any value of n the triangles are similar triangles.
Similar triangles have different sizes but the correpondign angles are the same (are congruent).
As triangles with sides 5n, 12n, 13n are similar triangles (All of then have the same measure on his correspondig angles) and makes true the Pythagorean theorem, they are right triangles.