Question

Each ticket to a matinee movie costs $8. Part A: Complete this table relating the number of movie tickets bought, m, to the total cost, c, of the tickets. m C 4 6 9 Part B: Write an equation that models this situation, using the variables m and c. Answer: Brandy thinks the number of movie tickets bought depends on the total cost of the movie tickets. Brandy's brother thinks the total cost of the movie tickets depends on the number of movie tickets bought Part C: Whose thinking is correct, Brandy's, her brother's, or both? Explain how you know.

Answer 1

Part A

Since each ticket costs $8, we need to add $8 for each plus ticket one buys:

`\begin{gathered} 1\text{ ticket: \$}8 \\ 2\text{ tickets: \$}8+\text{ \$}8=\text{ \$}16 \\ 3\text{ tickets: \$}16+\text{ \$}8=\text{ \$}24 \\ 4\text{ tickets: \$}24+\text{ \$}8=\text{ \$}32 \\ 6\text{ tickets: \$}32+\text{ \$}16=\text{ \$}48 \\ 9\text{ tickets: \$}48+\text{ \$}24=\text{ \$}72 \end{gathered}`

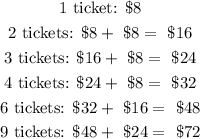
Therefore, we have:

Part B

Notice that, instead of summing (8+8+8+...) we can multiply $8 by the number of tickets bought m to obtain the total cost c.

Thus, we have:

`c=m*\text{ \$}8`

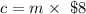
Part C

The equation above (c = m x $8) shows that the total cost c depends on the number of tickets bought.

However, we write that relation in another way:

`m=c/\text{ \$}8`

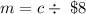
Thus, if we know the total cost, we can divide it by $8 to find the number of tickets bought. Then, we can say that the number of tickets boght m depends on the total cost c.

Therefore, both thoughts are correct.