Question

Sketch a line of best fit: The graph shows the depth y in centimeters of water filling a bathtub after x minutes. An equation for this line of best fit could be y = 2.4x-3.2. Use the sketch tool to sketch the line of best fit. A) interpolate: Use the given data to determine how much water is in the tub after 7 min. B) Extrapolate: Use the model (your equation) to predict the amount of water in the tub after 30 min. (Extrapolate means you are outside the known data.) I just want to make sure I created the line of best fit and that my answers to each question are correct.

Answer 1

The given equation of the line that best fits the data is:

`y=\text{2}.4x-3.2`

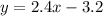
In order to graph it we can solve the equation for different x-values, and then find the coordinates of the points to draw the line.

For x=2, the y-value is:

`\begin{gathered} y=2.4\cdot2-3.2 \\ y=4.8-3.2 \\ y=1.6 \end{gathered}`

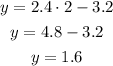
For x=7, the y-value is:

`\begin{gathered} y=2.4\cdot7-3.2 \\ y=16.8-3.2 \\ y=13.6 \end{gathered}`

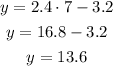
And for x=12, the y-value is:

`\begin{gathered} y=2.4\cdot12-3.2 \\ y=28.8-3.2 \\ y=25.6 \end{gathered}`

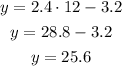
Then, by placing these 3 points in the coordinate plane, we can draw the line, as follows:

The graph with the given points is:

b. Interpolate: the water is in the tube after 7 minutes 13.6 centimeters. We have already made the calculation in part a. When x=7, then y=13.6

c. Extrapolate: the amount of water after 30 minutes will be:

`\begin{gathered} y=2.4\cdot30-3.2 \\ y=68.8 \end{gathered}`

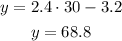
The predicted amount of water after 30 minutes will be 68.8 centimeters.