The given equation of the line that best fits the data is:
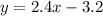
In order to graph it we can solve the equation for different x-values, and then find the coordinates of the points to draw the line.
For x=2, the y-value is:
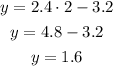
For x=7, the y-value is:

And for x=12, the y-value is:
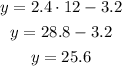
Then, by placing these 3 points in the coordinate plane, we can draw the line, as follows:
The graph with the given points is:
b. Interpolate: the water is in the tube after 7 minutes 13.6 centimeters. We have already made the calculation in part a. When x=7, then y=13.6
c. Extrapolate: the amount of water after 30 minutes will be:
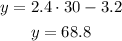
The predicted amount of water after 30 minutes will be 68.8 centimeters.