Question

Z-SCORES3. Suppose the speeds of cars on a street are normally distributed,with a mean of 76.4 kph and a standard deviation of 5.0 kph.Part A: To the nearest tenth of a percent, what is the probabilitythat a car is going slower than 70 kph? (3 points: 2 points forcorrectly finding the probability and 1 point for expressing theanswer to a tenth of a percent)Part B: To the nearest tenth of a percent, what is the probabilitythat a car is going faster than 80 kph? (4 points: 3 points forcorrectly finding the probability and 1 point for expressing theanswer to a tenth of a percent)Part C: To the nearest tenth of a percent, what is the probabilitythat a car is going between 72 kph and 78 kph? (7 points: 6points for correctly finding the probability and 1 point forexpressing the answer to a tenth of a percent)

Answer 1

Part A: Probability of a car going slower than 70 kph, The probability is approximately 10.0%.

Part B: Probability of a car going faster than 80 kph, The probability is approximately 23.6%.

Part C: Probability of a car going between 72 kph and 78 kph, The probability is approximately 43.7%.

Given:

Mean
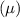`(\(\mu\))` = 76.4 kph

Standard deviation
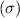`(\(\sigma\))` = 5.0 kph

Part A: Probability of a car going slower than 70 kph

First, let's find the z-score for 70 kph:

`\[ Z = (X - \mu)/(\sigma) \]`

`\[ Z = (70 - 76.4)/(5) = (-6.4)/(5) = -1.28 \]`

Using a standard normal distribution table or a calculator, the probability corresponding to Z = -1.28 is approximately 0.1003, or 10.03% (rounded to the nearest tenth of a percent).

Part B: Probability of a car going faster than 80 kph

Let's find the z-score for 80 kph:

`\[ Z = (80 - 76.4)/(5) = (3.6)/(5) = 0.72 \]`

From the standard normal distribution table or a calculator, the probability corresponding to Z = 0.72 is approximately 0.7642, or 76.42% (rounded to the nearest tenth of a percent).

To find the probability of going faster than 80 kph, subtract this probability from 100%:

Probability = 100% - 76.42% = 23.58% (rounded to the nearest tenth of a percent).

Part C: Probability of a car going between 72 kph and 78 kph

For 72 kph:

`\[ Z_(72) = (72 - 76.4)/(5) = (-4.4)/(5) = -0.88 \]`

For 78 kph:

`\[ Z_(78) = (78 - 76.4)/(5) = (1.6)/(5) = 0.32 \]`

Using the z-table:

- At Z = -0.88, the cumulative probability is approximately 0.1884.

- At Z = 0.32, the cumulative probability is approximately 0.6255.

The probability between 72 kph and 78 kph is the difference between these cumulative probabilities:

Probability = 0.6255 - 0.1884 = 0.4371 or 43.71% (rounded to the nearest tenth of a percent).

Answer 2

The Solution.

Z-score formula is given as below:

`Z=(x-\mu)/(\sigma)`

In this case,

`x=70,\mu=76.4,\sigma=5`

Therefore,

`Z=(70-76.4)/(5)=-(6.4)/(5)=-1.28`

Hence, using the negative z-score table, we have

`Pr(Z<-1.28)=0.1003`

Hence, the probability for part A is 10.0%

For part B:

First, we find the z-score of 80

`\begin{gathered} \text{ the value of x now becomes} \\ x=80 \\ \text{ thus} \\ z=(80-76.4)/(5)=(3.6)/(5)=0.72 \end{gathered}`

Hence, using the positive z-score table, we have

`Pr(Z>0.72)=1-Pr(Z\le0.72)=1-0.7642=0.2358`

Therefore, the probability for part B is 23.6%

For part C:

First, we find the z-score of 72 and 78

`\begin{gathered} when\text{ the value of x becomes} \\ x=72 \\ \text{ thus} \\ z=(72-76.4)/(5)=(-4.4)/(5)=-0.88 \end{gathered}`

`\begin{gathered} when\text{ the value of x becomes} \\ x=78 \\ \text{ thus} \\ z=(78-76.4)/(5)=(1.6)/(5)=0.32 \end{gathered}`

Hence, using the positive z-score table, we have

[tex]Pr(-0.88

Therefore, the probability for part C is 43.6%