Given,
The length of the string, L=0.85 m
The diameter of the string, d=6×10⁻⁴ m
The radius of the string, r=3×10⁻⁴ m
The Young's Modulus of the string, Y=190 GPa
The tension, F=66 N
a)
The Young's Modulus is given by,
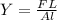
Where A is the area of cross-section of the string and l is the extension produced in the string.
On rearranging the above equation,
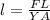
On substituting the known values,
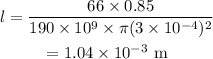
Thus the extension of the wire that is needed to be produced is 1.04×10⁻³ m
b)
The work done in producing the extension is given by,

On substituting the known values,
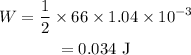
Thus the work done in producing the extension is 0.034 J