Question

Give any values of x that need to be excluded from f(g(x)). Select the correct choice below and fill in any answer boxes within your choice.

Answer 1

Step-by-step explanation:

Given the below functions;

`\begin{gathered} f(x)=4x-3 \\ g(x)=(1)/(4)(x+3) \end{gathered}`

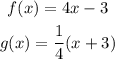
a) We're to find f(g(x)).

To do this, we need to substitute x in f(x) with g(x) as shown below;

`\begin{gathered} f(g(x))=4\lbrack(1)/(4)(x+3)\rbrack-3 \\ =(x+3)-3 \\ =x \end{gathered}`

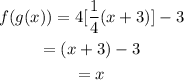
b) To find g(f(x)), we need to substitute x in g(x) with f(x);

`\begin{gathered} g(f(x))=(1)/(4)\lbrack(4x-3)+3\rbrack \\ =(1)/(4)(4x) \\ =x \end{gathered}`

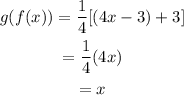
c) Since f(g(x)) = g(f(x)) = x, therefore f and g are inverses of each other.

Yes, f and g are inverses of each other.

So to