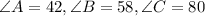Given
The sides of a triangle,
a=25cm, b=32cm & c=37cm.
To solve the oblique triangle ABC.
Step-by-step explanation:
It is given that,
The sides of a triangle,
a=25cm, b=32cm & c=37cm.
That implies,
By using cosine law,
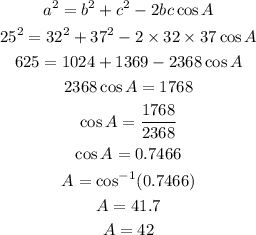
Also,
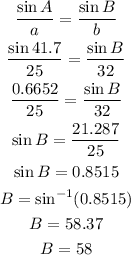
Therefore,
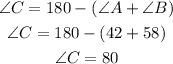
Hence,
The answers are,