Step-by-step explanation
Step 1
parent function:
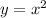
and the transformed function is
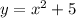
hence ,

we can see that 5 was added to the parent function to get the actual function, so
transformation : 5 was added
: To move a function up, you add outside the function: f (x) + b is f (x) moved up b units
so we can conclude:
the function was shifted 5 units up
Step 2
get the vertex form:
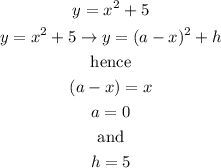
therefore, the vertex is

Step 3
orientation :
The orientation of a quadratic function is determined solely by the coefficient ax^2+bx+c=0. If this coefficient is positive, the parabola opens up. If this coefficient is negative, the parabola opens down
so, let's check

the parabola opens up
Step 3
horizontal shift:
Given a function f, a new function g(x)=f(x−h), where h is a constant, is a horizontal shift of the function f. If h is positive, the graph will shift right. If h is negative, the graph will shift left.
we can see that in the argument nothing was added, so
there is not horizontal shift
I hope this helps you