First, we are going to calculate the area of the semicircle.
The area of a circle is given by the following expression:
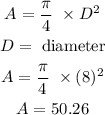
As in the figure we have a semicircle, we have to divide the value of the Area by 2,

Now we have to calculate the area of the trapezoid,
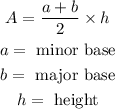
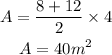
Now we add both values, area of the semicircle and area of the trapezoid,

Answer= 65.13 square meters